J’avais déjà fait un furet des grands nombres pour familiariser les élèves avec les opérations de lecture / verbalisation des grands nombres. C’est un excellent exercice de lecture décodage pour celui qui lit, écoute encodage et comparaison pour ceux qui écoutent que j’ai eu besoin d’adapter pour mes élèves de cycle 2. J’en ai profité pour traiter toutes les classes de nombres afin d’être exhaustif, vous trouverez donc en bas de page des fichiers pour les nombres jusqu’à 100, 1000, 10000 et 100000.
Principes et utilisation
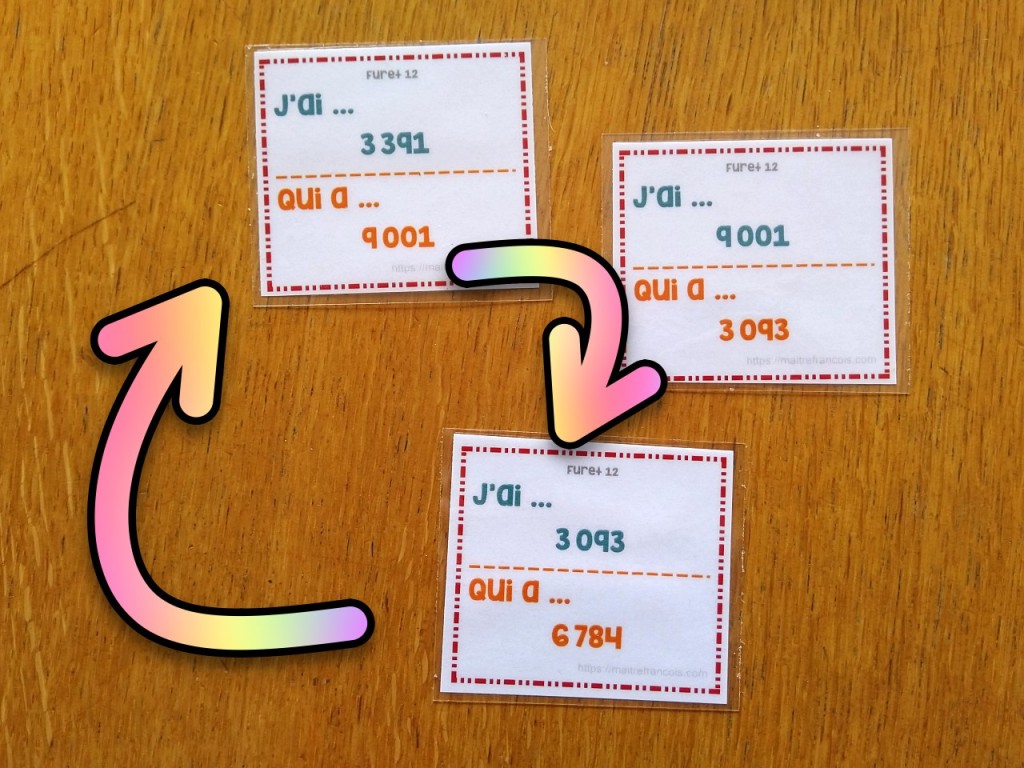
Comme je l’expliquais dans l’article sur le furet des grands nombres, un des problèmes avec les furets que j’ai trouvés tous faits sur Internet c’est qu’on ne sait jamais vraiment à quel moment s’arrêter… Il faut vérifier que tout le monde soit passé et être sûr de ne pas avoir d’élève avec une carte « impasse ». C’est la raison d’être des fichiers que je vous propose ici : la suite de nombres est circulaire, c’est à dire telle que la dernière carte appelle la première. Ça marche à tous les coups !
Pour que le furet fonctionne correctement, il suffit d’imprimer le jeu qui correspond à son nombre d’élèves. Il suffit alors de distribuer les cartes, choisir un élève au hasard et de continuer le jeu tant qu’on n’est pas revenu au premier joueur.
Les fichiers sont prévus pour des classes de 12 à 32 élèves :
- Classe des unités de 0 à 99
- Classe des unités de 0 à 999
- Classe des mille de 1000 à 9999
- Classe des mille de 1000 à 99999
- Classe des mille de 1000 à 999999
Dans chaque fichier, il y a 4 niveaux de difficulté (matérialisés par des couleurs allant du vert au noir). J’ai en effet constaté que les élèves avaient des difficultés avec les 71, 72 … 99 et les nombres contenant des 0 comme 1032 où l’absence de centaine ne donne pas lieu à une prononciation. Ces difficultés sont donc introduites progressivement dans les différents niveaux de difficulté.
Les niveaux de difficulté sont tels que :
- Niveau vert : suite de nombres de la classe considérée. On y évite les 70, 80 et 90 qui peuvent poser des soucis de lecture et les nombres contenant des 0.
- Niveau bleu : quelques zéros et 80 font leur apparition pour complexifier la lecture.
- Niveau rouge : encore plus de zéros, des 70, 80 et 90 pour rendre la lecture encore plus complexe.
- Niveau noir : à la difficulté précédente s’ajoute le fait que les classes de nombres ne sont plus séparées par des espaces.
A l’utilisation c’est très classique (et simple) : chaque élève reçoit une carte, un élève choisi au hasard commence la lecture de sa carte « J’ai … , qui a … » et on continue jusqu’à avoir fait la boucle jusqu’à l’élève de départ.
Fichiers à télécharger
Les fichiers sont disponibles ci-dessous. Ils sont assez volumineux mais il vous suffit d’imprimer les pages qui correspondent à votre nombre d’élèves (voir la table des matières dans chaque fichier pour vous repérer) puis de plastifier les cartes :
- Furet des nombres – Classe des unités – 0 à 99 – De 12 à 32 élèves.pdf
- Furet des nombres – Classe des unités – 0 à 999 – De 12 à 32 élèves.pdf
- Furet des nombres – Classe des mille – 1000 à 9999 – De 12 à 32 élèves.pdf
- Furet des nombres – Classe des mille – 1000 à 99999 – De 12 à 32 élèves.pdf
- Furet des nombres – Classe des mille – 1000 à 999999 – De 12 à 32 élèves.pdf